While computers have transformed chess analysis—most famously with Deep Blue’s victory over Garry Kasparov in 1997—the game remains “unsolved.” Stockfish and AlphaZero dominate as chess engines, but even they rely on approximations and do not guarantee perfect play from start to finish. Can quantum computers solve chess?
So, what would it mean to truly “solve” chess? Would it involve discovering a perfect strategy for every position, or mapping out all possible outcomes from the first move? The answer is not straightforward and touches on deep computational and philosophical questions.
Quantum computing, with its ability to process information differently from classical computers, offers a potential breakthrough. Could it finally untangle the complexity of chess, where trillions of possibilities arise from just a few moves? In this article, we explore what “solving” chess entails, analyze the game’s inherent computational challenges, and examine whether quantum computers might hold the answer.
1. What would “Solve” chess mean?
Solving chess under perfect play involves determining the exact outcome of the game if both players make optimal moves at every turn. A perfect game assumes that each player follows a flawless strategy to maximize their own chances of winning or drawing while avoiding losing positions. The nature of a perfect game differs slightly for white and black, reflecting the dynamics of their roles.
For white, a perfect game means capitalizing on the first-move advantage. White’s optimal strategy is to either secure a win or force a draw if black defends perfectly. White’s perfect play ensures that it avoids any mistakes that could give black an opportunity to win.
For black, a perfect game is focused on defense. Starting second, black aims to neutralize white’s initiative. Black’s perfect play involves forcing a draw at minimum, and exploiting any suboptimal moves by white to secure a win. However, against perfect white play, black cannot win and can at best force a draw.
Thus, the ultimate outcome of a perfectly played chess game is either a draw or a win for white, as black cannot overcome white’s first-move advantage under flawless conditions.
| White’s Play | Black’s Play | Outcome | Explanation |
|---|
| Perfect | Perfect | Draw or White Win | White’s first-move advantage ensures black cannot win. |
| Perfect | Imperfect | White Win | Black’s suboptimal moves allow white to exploit its advantage and secure a win. |
| Imperfect | Perfect | Black Win | Black capitalizes on white’s mistakes and gains a winning position. |
2. Understanding Chess Complexity
Chess is a deceptively simple game with rules that are easy to learn but lead to staggering complexity. At its core, chess is a finite, deterministic game, meaning there is a limited number of legal moves and positions. However, the number of possible games is so immense that it far exceeds the computational capacity of modern classical computers.
The game-tree complexity of chess, which represents the total number of possible games from the initial position, is estimated to be around 1012010^{120}10120. This number, called the Shannon Number, dwarfs the number of atoms in the observable universe. Each move branches into new possibilities, creating an exponential explosion in potential positions after just a few moves.
Chess also has a state-space complexity, the total number of legal board positions, which is estimated to be around 104010^{40}1040. While smaller than the game-tree complexity, this figure still presents a monumental challenge for computational approaches.
The difficulty of solving chess lies in evaluating these positions. Unlike simpler games like checkers, where all positions have been mapped to outcomes (win, lose, draw), chess positions are evaluated by engines like Stockfish and AlphaZero using heuristics and machine learning. These engines search millions of positions per second but still cannot guarantee perfect play due to practical computational limits.
Adding to this complexity is the 50-move rule and threefold repetition, which impose draw conditions, further complicating the task of analyzing positions. Additionally, the presence of tactics, strategies, and long-term planning makes many positions challenging to evaluate even for advanced engines.
The vast branching factor of chess, combined with the need for deep evaluation of moves, has made it a benchmark for computational problem-solving. Solving chess would mean navigating this immense complexity to definitively determine the outcome of every possible position under perfect play. This computational challenge underscores why chess remains unsolved, even as classical computing continues to advance.
The Basics of Quantum Computing
Quantum computing is a revolutionary field that leverages the principles of quantum mechanics to process information in ways that classical computers cannot. Unlike classical bits, which can be either 0 or 1, quantum bits (qubits) can exist in a superposition of states, representing both 0 and 1 simultaneously. This allows quantum computers to process vast amounts of information in parallel, making them well-suited for problems involving immense complexity, like chess.
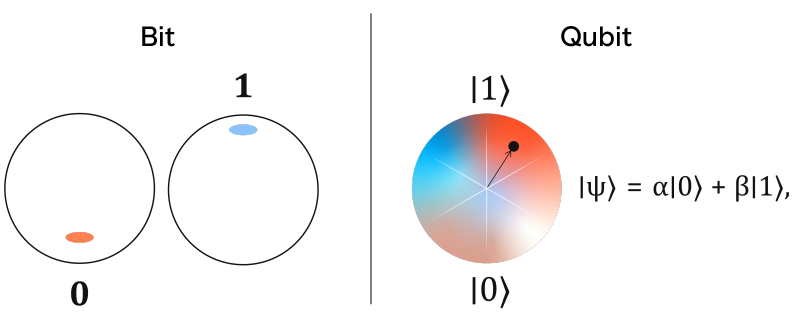
Quantum computing’s power comes from superposition, entanglement, and quantum interference. Superposition enables qubits to explore multiple possibilities simultaneously, while entanglement allows qubits to correlate their states instantaneously across distances. These properties offer a potential exponential speedup for solving certain computational problems.
A rough estimate suggests that analyzing a single position with full quantum parallelism might require 40 to 50 qubits, as each qubit can encode two states. However, solving the game entirely, considering all possible moves and outcomes, would require qubits to encode the full game-tree complexity. This could push the requirement to over 120 qubits, depending on how efficiently quantum algorithms can structure and simplify the problem.
Current quantum computers, like IBM’s Eagle processor (127 qubits), are approaching these numbers, but issues like quantum noise and error correction significantly reduce the usable qubits. To solve chess definitively, researchers would likely need fault-tolerant quantum computers with thousands of physical qubits to support the necessary logical qubits.
Challenges of Applying Quantum Computing to Chess
Solving chess with quantum computing is theoretically possible but remains a distant goal due to the immense complexity of the game. Chess, as a finite game, can be solved by determining whether the outcome under perfect play is a win for white or a draw. With 104010^{40}1040 legal positions and 1012010^{120}10120 possible games, solving chess requires computational power far beyond the capabilities of classical computers. Quantum computing, with its ability to explore multiple possibilities simultaneously, provides a promising path forward. However, the necessary hardware and algorithms are still in their infancy.
Today’s quantum systems, such as IBM’s 127-qubit Eagle processor and Google’s 72-qubit Sycamore, showcase major advancements but are limited by quantum noise, short coherence times, and inadequate error correction. Google’s next-generation processor, Willow, is expected to improve on scalability and error resistance, bringing us closer to fault-tolerant quantum computing. However, solving chess requires millions of physical qubits to support thousands of error-corrected logical qubits, far exceeding current capabilities.

Quantum algorithms present another challenge. While algorithms like Grover’s search provide speedups for specific problems, they are not designed for chess’s intricate game trees and evaluation of positions. Specialized quantum algorithms tailored to chess’s branching complexity and strategic depth are essential. Additionally, solving chess involves more than brute force; it requires accurate evaluation of positions—a task where classical AI, like AlphaZero, currently excels.
Predictions for when chess might be solved with quantum computing:
- 5 to 15 years: Quantum systems like Google Willow could enable breakthroughs in smaller-scale problems, such as solving complex endgames or specific branches of the game tree.
- 15 to 30 years: Fault-tolerant quantum computers with thousands of logical qubits may become viable, enabling significant progress in tackling chess’s vast complexity.
- 50 to 100 years: Fully solving chess, including mapping all positions and determining the perfect outcome under ideal play, could become achievable with advanced hardware and refined algorithms.
Conclusion
In conclusion, solving chess with quantum computing is a tantalizing possibility, but it remains decades away. The game’s immense game-tree complexity and state-space complexity push even the most advanced quantum systems to their limits. Current quantum computers, like Google’s Willow (104 qubits) and IBM’s Eagle (127 qubits), are far from the fault-tolerant systems required to tackle chess’s vast complexity. Solving chess entirely would likely require millions of physical qubits to create the thousands of error-corrected logical qubits necessary for reliable calculations.
Predictions suggest that within 5 to 15 years, advancements in quantum hardware, such as Google Willow, may allow breakthroughs in solving smaller components of chess, such as complex endgames. By 15 to 30 years, fault-tolerant quantum computers with thousands of logical qubits could handle larger portions of chess’s game tree, potentially solving limited scenarios. Fully solving chess, however, including mapping all possible games and positions, may take 50 to 100 years or more, depending on the pace of innovation.
The implications of solving chess are profound. If perfect play leads to a forced draw, it could shift focus from creativity to precision, much like what happened with checkers. Alternatively, if white has a guaranteed winning strategy, the solution could lead to fundamental rule changes or the creation of new chess variants to restore balance. Beyond chess, the pursuit of solving it will drive advancements in quantum algorithms, error correction, and computational theory, influencing broader fields like cryptography and optimization.
In the end, solving chess is not just about answering a question—it is about pushing the limits of technology and understanding. While we are still many decades away, each step toward this goal offers new insights into the interplay between computation, strategy, and the enduring mystery of chess.

